Metody numeryczne i probabilstyczne

poniedziałek, 17 grudnia 2012

Wielkie układy równań liniowych

Wraz z coraz większymi modelami pojawiającymi się w praktyce obliczeniowej, coraz częściej zachodzi potrzeba rozwiązywania zadań algebry liniowej, w której macierze są co prawda wielkiego wymiaru, ale najczęściej rozrzedzone, to znaczy jest w nich bardzo dużo zer. Bardzo często zdarza się, że macierz wymiaru $\displaystyle N$ ma tylko $\displaystyle O(N)$ niezerowych elementów. Wykorzystanie tej specyficznej własności macierzy nie tylko prowadzi do algorytmów istotnie szybszych od ich analogów dla macierzy gęstych (to znaczy takich, które (w założeniu) mają $\displaystyle N^2$ elementów), ale wręcz są jedynym sposobem na to, by niektóre zadania w ogóle stały się rozwiązywalne przy obecnym stanie techniki obliczeniowej!

Czynnik rozkładu Cholesky'ego $\displaystyle L$ wykonanego standardowym algorytmem. Czas rozkładu: 0.892013

Macierz rozrzedzona (Octave):
<realnowiki><realnowiki><realnowiki><realnowiki>octave:10> I = [1, 1, 1, 2, 3, 1, 4]; octave:11> J = [1, 3, 2, 2, 3, 4, 4]; octave:12> V = [1, 2, 3, 4, 5, 6, 7]; octave:13> N = 4; octave:14> A = sparse(I,J,V,N,N) A = Compressed Column Sparse (rows = 4, cols = 4, nnz = 7) (1, 1) -> 1 (1, 2) -> 3 (2, 2) -> 4 (1, 3) -> 2 (3, 3) -> 5 (1, 4) -> 6 (4, 4) -> 7 octave:15> spy(A); </realnowiki></realnowiki></realnowiki></realnowiki>

(http://osilek.mimuw.edu.pl/index.php?title=MN08)

Macierze taśmowe

Macierz $\displaystyle A$ taka, że dla $\displaystyle |i-j| \geq d$ , $\displaystyle a_{ij} = 0$ , nazywamy macierzą taśmową z rozstępem $\displaystyle d$ , o szerokości pasma $\displaystyle 2d+1$ .

Łatwo sprawdzić, że algorytm eliminacji Gaussa (bez wyboru elementu głównego) nie spowoduje dodatkowego wypełnienia w takiej macierzy (a więc da się wykonać w miejscu). W przypadku konieczności wyboru elementu głównego, pesymistyczne oszacowanie rozstępu macierzy rozkładu LU jest równe $\displaystyle \max\{2d,N\}$ --- tak więc, dla niezbyt dużych $\displaystyle d$ wciąż wynikowa macierz jest taśmowa.

W szczególności, gdy macierz jest taśmowa z pasmem o rozstępie $\displaystyle d$ i jednocześnie diagonalnie dominująca, wtedy rozkład LU takiej macierzy da się wykonać w miejscu kosztem $\displaystyle O(d^2\,N)$ , czyli liniowym względem $N$ .

W LAPACKu zaimplementowano szybki solver równań z macierzami taśmowymi, DGBSV, ale wymagający specjalnego sposobu przechowywania macierzy, wykorzystującego format diagonalny.

Stacjonarne metody iteracyjne

Gdy macierz jest rozrzedzona, mnożenie takiej macierzy przez wektor jest bardzo tanie (koszt jest proporcjonalny do liczby niezerowych elementów macierzy). Dlatego, jeśli możemy zadowolić sięrozwiązaniem przybliżonym układu, a w zamian osiągnąć je tanim kosztem, warto rozważyć metody iteracyjne.

Najprostsze metody iteracyjne (najprostsze w analizie i implementacji, ale --- jak można się domyślić --- w praktyce najmniej efektywne) polegają na rozkładzie macierzy na część "łatwo odwracalną", $\displaystyle M$ , i "resztę", $\displaystyle Z$ . Dokładniej, jeśli $\displaystyle M$ jest nieosobliwa, to równanie $\displaystyle Ax = b$ można zapisać jako zadanie punktu stałego

$\displaystyle Mx = Zx + b,$

gdzie $\displaystyle Z=M-A$ . Inaczej:

$\displaystyle x = M^{-1}(Zx + b),$

i zastosować doń metodę iteracji prostej Banacha:

$\displaystyle x_{k+1} = M^{-1}(Zx_k + b).$

Takie metody nazywamy stacjonarnymi metodami iteracyjnymi. Aby przeanalizować zbieżność takiej metody, warto rozpatrzyć przypadek ogólniejszy

$\displaystyle x_k\,=\,B x_{k-1}\,+\, c,$

dla pewnej macierzy $\displaystyle B$ oraz wektora $\displaystyle c$ . (Dla stacjonarnej metody iteracyjnej, $\displaystyle B=M^{-1}Z$ oraz $\displaystyle c=M^{-1}b$ .)

W tym przypadku

$\displaystyle x_k- x^*\,=\,B^k( x_0- x^*),$

a stąd i z nierówności $\displaystyle \|B^k\|\le\|B\|^k$ , mamy

$\displaystyle \| x_k- x^*\|\,\le\, \|B\|^k\| x_0- x^*\|.$

Warunkiem dostatecznym zbieżności iteracji prostych jest więc $\displaystyle \|B\|<1$ . Okazuje się, że warunkiem koniecznym i dostatecznym zbieżności tej iteracji dla dowolnego wektora startowego $\displaystyle x_0$ jest

$\displaystyle \rho = \max\{ |\lambda| : \lambda \mbox{ jest wartością własną } B\} < 1.$

Tak więc, metody oparte na iteracji prostej będą zbieżne liniowo z ilorazem $\displaystyle \rho$ .

Zaletą stacjonarnych metod iteracyjnych jest również ich prostota, przez co są one łatwe do zaprogramowania, co łatwo zobaczyć na przykładach metod: Jacobiego i Gaussa--Seidela, które teraz omówimy.

poniedziałek, 10 grudnia 2012

Funkcje Statystyczne - excel

poniedziałek, 3 grudnia 2012

Statystyka Opisowa

Statystyka opisowa to dział statystyki zajmujacy sie metodami opisu danych statystycznych
(np. srodowiskowych) uzyskanych podczas badania statystycznego (
p. badan terenowych,
laboratoryjnych).
Badanie statystyczne to proces pozyskiwania danych na temat rozkładu cechy statystycznej
w populacji.
Populacja statystyczna – zbiór elementów, podlegajacych badaniu statystycznemu.
Elementy populacji sa do siebie podobne pod wzgledem badanej cechy, ale nie sa identyczne.
Przykład: Wszyscy studenci na Wydziale Geologii posiadaja ceche wzrostu - sa pod tym
wzgledem podobni, ale nie identyczni: sa studenci wysocy i niscy. Populacja w badaniu
statystycznym wzrostu studentów Geologii beda wszyscy studenci na Wydziale Geologii.
Próba losowa – wybrane losowo elementy populacji. Np. my na zajeciach.
Nie wszystkie populacje musza istniec w rzeczywistosci, niektóre z nich maja charakter
wyłacznie hipotetyczny.
Elementy populacji statystycznej nazywamy jednostkami statystycznymi, zas badana cecha to
cecha statystyczna.
Ze wzgledu na liczebnosc zbioru, populacje mo,na podzielic na:
populacje skonczone - np. populacja studentów Geologii
populacje nieskonczone - np. czas
Poniewa, czesto badanie statystyczne całej populacji jest nieuzasadnione lub niemo,liwe
(przyczyny: patrz badanie statystyczne), dlatego zwykle bada sie jedynie wybrane losowo
elementy populacji, czyli próbe losowa, a nastepnie wnioskuje na podstawie obserwacji
cechy w próbie o mo,liwych wartosciach cechy w populacji. Dlatego własnie niektóre pojecia
statystyczne moga odnosic sie zarówno do populacji, jak i do próby (sa to tzw. wielkosci
empiryczne).
Estymacja - szacowanie wartosci nieznanych parametrów rozkładu na podstawie znanych
wyników próby (mo,e byc stosowane jedynie w przypadku regularnych rozkładów
parametrów cechy w populacji).
Badanie statystyczne mo,e miec charakter:
pełny - badanie obejmuje cała populacje
czesciowy - odbywa sie na pewnych (zazwyczaj losowo) wybranych elementach populacji,
czyli próbie losowej, zazwyczaj reprezentatywnej dla populacji
W ramach badania statystycznego zbierane sa wartosci okreslonej cechy statystycznej
nazywane wartosciami zaobserwowanymi cechy statystycznej lub danymi
statystycznymi. Zró,nicowanie wartosci cechy statystycznej powoduje, ,e mo,na mówic o
jej rozkładzie w populacji (próbie losowej).
Próba reprezentatywna – czesc populacji, wybrana do badania metodami statystycznymi, w
zało,eniu badacza, zachowujaca strukture wyró,nionych cech populacji przy zało,onym
poziomie istotnosci.
Poziom istotnosci – % – okresla maksymalne ryzyko błedu, jakie badacz jest skłonny
zaakceptowac. Wybór wartosci . zale,y od badacza, natury problemu i od tego jak dokładnie
chce on weryfikowac swoje hipotezy, najczesciej przyjmuje sie . = 0,05 lub 0,01 czyli
obliczamy cos z 95 lub 99% prawdopodobienstwem.
Celem stosowania metod statystyki opisowej jest podsumowanie zbioru danych (np. próby
losowej) i wyciagniecie pewnych podstawowych wniosków i uogólnien na temat zbioru.
Statystyke opisowa stostosuje suje sie zazwyczaj jako pierwszy i podstawowy krok w analizie
zebranych danych

.
TESTY
www.wazniak.mimuw.edu.pl

Polecana książka :

poniedziałek, 19 listopada 2012

Aproksymacja

Procesy losowe

Proces stochastyczny to funkcja losowa, czyli funkcja matematyczna, której wartości leżą w przestrzeni zdarzeń losowych. Innymi słowy pewnej wielkości (jakiemuś człowiekowi, liczbie, chwili czasu, punktowi płaszczyzny) przypisane jest zdarzenie losowe (wzrost, losowo wybrana liczba, wartość waluty wg. notowań giełdowych, liczba rzeczywista).
Najprostszym przykładem procesu stochastycznego jest wielokrotny rzut monetą: dziedziną funkcji jest zbiór liczb naturalnych (ilość rzutów), natomiast wartością funkcji dla danej liczby jest jeden z dwóch możliwych stanów losowania (zdarzenie), orzeł lub reszka. Nie należy mylić procesu losowego którego wartości są zdarzeniami losowymi z funkcją która zdarzeniom przypisuje wartość prawdopodobieństwa ich wystąpienia (mamy wówczas do czynienia z rozkładem gęstości prawdopodobieństwa).
W praktyce dziedziną, na której zdefiniowana jest funkcja, jest najczęściej przedział czasowy (taki proces stochastyczny nazywany jest szeregiem czasowym) lub obszar przestrzeni (wtedy nazywany jest polem losowym). Jako przykłady szeregów czasowych można podać: fluktuacje giełdowe, sygnały, takie jak mowa, dźwięk i wideo, dane medyczne takie jak EKG i EEG, ciśnienie krwi i temperatura ciała, losowe ruchy takie jak ruchy Browna. Przykładami pól losowych są statyczne obrazy, losowe krajobrazy i układ składników w niejednorodnych materiałach.

Definicja

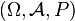Niech $T$ będzie niepustym zbiorem, który będziemy dalej nazywać zbiorem indeksów, $(\Omega, \mathcal{A}, P)$ będzie przestrzenią probabilistyczną oraz $(E, \mathfrak{M})$ będzie przestrzenią mierzalną. Rodzinę zmiennych losowych

$X=(X_t)_{t\in T}$ ,

to znaczy rodzinę funkcji $\mathcal{A}/\mathfrak{M}$ - mierzalnych nazywamy procesem stochastycznym. Przestrzeń $(E, \mathfrak{M})$ nazywamy przestrzenią fazową albo przestrzenią stanów procesu $X$ .
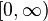Często za zbiór $T$ przyjmuje się przedział $[0,\infty)$ lub zbiór liczb naturalnych, za $E$ zbiór liczb rzeczywistych, a za $\mathfrak{M}$ rodzinę $\mathcal{B}(\mathbb{R})$ , to znaczy rodzinę borelowskich podzbiorów prostej.
Procesy stochastyczne, których zbiór indeksów jest przeliczalny nazywamy łańcuchami.

Ciekawostka.
Ruchy Browna − chaotyczne ruchy cząstek w płynie (cieczy lub gazie), wywołane zderzeniami zawiesiny z cząsteczkami płynu.
W 1827 roku szkocki biolog Robert Brown obserwując przez mikroskop pyłki kwiatowe w zawiesinie wodnej dostrzegł, iż znajdują się one w nieustannym, chaotycznym ruchu.
Ruchy Browna obserwuje się dla mikroskopijnych, mniejszych niż mikrometr, cząstek zawiesiny bez względu na ich rodzaj. Cząsteczki poruszają się ciągle, a ich ruch nie słabnie. Prędkość ruchu jest większa dla mniejszych cząstek i wyższej temperatury.